squ1rrel CTF 2024
https://ctftime.org/event/2370
CHALL’S SOLVED
| Category | Challenge |
|---|---|
| Crypto | Lazy RSA |
| Crypto | RSA RSA RSA |
| Misc | rainbolt0 |
| Rev | Secret Coffee Nut Stash |
| Rev | PYC Fun |
Crypto
Lazy RSA
Overview
Description: Generating primes is too hard, but I did find a couple posted online!
This is the most common RSA challenges:
- n: the modulus for both the public and private keys
- e: the public exponent
- ct: the ciphertext want to decrypt
n: 23690620655271165329693230765997410033604713853187305472268813793031152348107488119317901392104240429826482611449247251262846508667797483465355228800439339041030982259847598574606272955688345490638311164838117491821117626835340577511562130640807587611523935604871183668968359720411023759980144229161581597397061850707647104033348795132205561234674677139395868595692235525931999596382758921793937149945229459379437008216713404350896206374483356969246476531491049930769999387038678280465689487577291475554699094024761030833540509263174840007922218340417888061099317752496279552046029470370474619439450870110783844218281
e: 65537
ct: 11420169733597912638453974310976296342840438772934899653944946284527921765463891354182152294616337665313108085636067061251485792996493148094827999964385583364992542843630846911864602981658349693548380259629884212903554470004231160866680745154066318419977485221228944716844036265911222656710479650139274719426252576406561307088938784324291655853920727176132853663822020880574204790442647169649094846806057218165102873847070323190392619997632103724159815363319643022552432448214770378596825200154298562513279104608157870845848578603703757405758227316242247843290673221718467366000253484278487854736033323783510299081405To solve this, we will factor {n} into two prime numbers, {p} and {q}. Typically this phase is the most time consuming, especially if {n} is a large number. As in the challenge description, according to challenge description “Generating primes is too hard, but I did find a couple posted online!” by using factorization tools available online such as FactorDB.
Once we get the factor n. Here’s a possible step to check whether p and q are indeed factors of n.
n = 23690620655271165329693230765997410033604713853187305472268813793031152348107488119317901392104240429826482611449247251262846508667797483465355228800439339041030982259847598574606272955688345490638311164838117491821117626835340577511562130640807587611523935604871183668968359720411023759980144229161581597397061850707647104033348795132205561234674677139395868595692235525931999596382758921793937149945229459379437008216713404350896206374483356969246476531491049930769999387038678280465689487577291475554699094024761030833540509263174840007922218340417888061099317752496279552046029470370474619439450870110783844218281
p = 136883787266364340043941875346794871076915042034415471498906549087728253259343034107810407965879553240797103876807324140752463772912574744029721362424045513479264912763274224483253555686223222977433620164528749150128078791978059487880374953312009335263406691102746179899587617728126307533778214066506682031517
q = 173071049014527992115134608840044450224804187710129859708853805709176487316207010402251651554296674942983458628001825388092613984020357016543095854903752286499436288875811897772811421580394898931781960982007306544027009178109074133665714245347548210688178519450728052309689045110008994598784658702110905581693
if p * q == n:
print("p * q == n")
else:
print("p * q != n")Final solver:
1from Crypto.Util.number import inverse, long_to_bytes
2
3# given values
4n = 23690620655271165329693230765997410033604713853187305472268813793031152348107488119317901392104240429826482611449247251262846508667797483465355228800439339041030982259847598574606272955688345490638311164838117491821117626835340577511562130640807587611523935604871183668968359720411023759980144229161581597397061850707647104033348795132205561234674677139395868595692235525931999596382758921793937149945229459379437008216713404350896206374483356969246476531491049930769999387038678280465689487577291475554699094024761030833540509263174840007922218340417888061099317752496279552046029470370474619439450870110783844218281
5e = 65537
6ct = 11420169733597912638453974310976296342840438772934899653944946284527921765463891354182152294616337665313108085636067061251485792996493148094827999964385583364992542843630846911864602981658349693548380259629884212903554470004231160866680745154066318419977485221228944716844036265911222656710479650139274719426252576406561307088938784324291655853920727176132853663822020880574204790442647169649094846806057218165102873847070323190392619997632103724159815363319643022552432448214770378596825200154298562513279104608157870845848578603703757405758227316242247843290673221718467366000253484278487854736033323783510299081405
7
8# factorized {n} with factordb.com
9p = 136883787266364340043941875346794871076915042034415471498906549087728253259343034107810407965879553240797103876807324140752463772912574744029721362424045513479264912763274224483253555686223222977433620164528749150128078791978059487880374953312009335263406691102746179899587617728126307533778214066506682031517
10q = 173071049014527992115134608840044450224804187710129859708853805709176487316207010402251651554296674942983458628001825388092613984020357016543095854903752286499436288875811897772811421580394898931781960982007306544027009178109074133665714245347548210688178519450728052309689045110008994598784658702110905581693
11
12phi = (p - 1) * (q - 1)
13d = inverse(e, phi)
14m = pow(ct, d, n)
15
16message = long_to_bytes(m)
17print(message)$ python3 solve.py
b'squ1rrel{laziness_will_be_the_answer_eventually}'FLAG
squ1rrel{laziness_will_be_the_answer_eventually}
RSA RSA RSA
Overview
Description: I had something so important to say that I just had to tell three of my friends!
This one is a RSA Chinese Remainder Theorem (CRT) challenge. From the provided chall source, we given three ciphertexts and three moduli, all encrypted with the same exponent {e}.
e: 3
n1: 96137714481560340073780038250015316564930752333880363375193088083653975552334517899735106334409092229494004991796910602440032630762575914714152238916128674595912438177270978040111855327624812652948702562503276973409716595778936978757384935820012322432156169815110042972411989274515686945691887468406312791931
ct1: 45640508926729498938915879450220374487095109122207451961200230820161694723491945276893630019713859109920025191680053056485030809079137883906737197875968862878423820820515399840094772412319820062860149582361429346029277273870654355752499436360499181221418835401103925420623212341317366954144592892392013649421
n2: 90990790933807553440094447797505116528289571569256574363585309090304380702927241663491819956599368816997683603352289726407304960362149545383683196526764288524742203975596414405902155486632888712453606841629050125783639571606440840246928825545860143096340538904060826483178577619093666337611264852255012241011
ct2: 58149644956871439128498229750735120049939213159976216414725780828349070974351356297226894029560865402164610877553706310307735037479690463594397903663323983980128060190648604447657636452565715178438939334318494616246072096228912870579093620604596752844583453865894005036516299903524382604570097012992290786402
n3: 86223965871064436340735834556059627182534224217231808576284808010466364412704836149817574186647031512768701943310184993378236691990480428328117673064942878770269493388776005967773324771885109757090215809598845563135795831857972778498394289917587876390109949975194987996902591291672194435711308385660176310561
ct3: 16168828246411344105159374934034075195568461748685081608380235707338908077276221477034184557590734407998991183114724523494790646697027318500705309235429037934125253625837179003478944984233647083364969403257234704649027075136139224424896295334075272153594459752240304700899700185954651799042218888117178057955By combining these equations and solving for the plaintext message, the solution makes use of the CRT. Here’s how to do it:
1from sympy import *
2from Crypto.Util.number import long_to_bytes
3
4# given values
5e = 3
6n1 = 96137714481560340073780038250015316564930752333880363375193088083653975552334517899735106334409092229494004991796910602440032630762575914714152238916128674595912438177270978040111855327624812652948702562503276973409716595778936978757384935820012322432156169815110042972411989274515686945691887468406312791931
7ct1 = 45640508926729498938915879450220374487095109122207451961200230820161694723491945276893630019713859109920025191680053056485030809079137883906737197875968862878423820820515399840094772412319820062860149582361429346029277273870654355752499436360499181221418835401103925420623212341317366954144592892392013649421
8n2 = 90990790933807553440094447797505116528289571569256574363585309090304380702927241663491819956599368816997683603352289726407304960362149545383683196526764288524742203975596414405902155486632888712453606841629050125783639571606440840246928825545860143096340538904060826483178577619093666337611264852255012241011
9ct2 = 58149644956871439128498229750735120049939213159976216414725780828349070974351356297226894029560865402164610877553706310307735037479690463594397903663323983980128060190648604447657636452565715178438939334318494616246072096228912870579093620604596752844583453865894005036516299903524382604570097012992290786402
10n3 = 86223965871064436340735834556059627182534224217231808576284808010466364412704836149817574186647031512768701943310184993378236691990480428328117673064942878770269493388776005967773324771885109757090215809598845563135795831857972778498394289917587876390109949975194987996902591291672194435711308385660176310561
11ct3 = 16168828246411344105159374934034075195568461748685081608380235707338908077276221477034184557590734407998991183114724523494790646697027318500705309235429037934125253625837179003478944984233647083364969403257234704649027075136139224424896295334075272153594459752240304700899700185954651799042218888117178057955
12
13# compute N = n1*n2*n3
14N = n1*n2*n3
15
16# compute Ni and yi for i in {1,2,3}
17N1 = N // n1
18y1 = pow(N1, -1, n1)
19N2 = N // n2
20y2 = pow(N2, -1, n2)
21N3 = N // n3
22y3 = pow(N3, -1, n3)
23
24# compute m^3 using CRT
25m_cubed = (ct1*N1*y1 + ct2*N2*y2 + ct3*N3*y3) % N
26
27# compute m by taking cube root of m^3
28m = root(m_cubed, 3)
29
30flag = long_to_bytes(m)
31
32print(flag)$ python3 solve.py
b'squ1rrel{math_is_too_powerful_1q3y41t1s98u23rf8}'FLAG
squ1rrel{math_is_too_powerful_1q3y41t1s98u23rf8}
Misc
rainbolt0
Overview
Description: Once you’ve tracked down the location find it on here: https://what3words.com/ and submit as the flag
example: squ1rrel{painting.impact.picture}
As per the description of the challenge, we were asked to find the landmark location of the image. Using Google Lens, we quickly located the "Parthenon" landmark and discovered that it corresponds to the image.
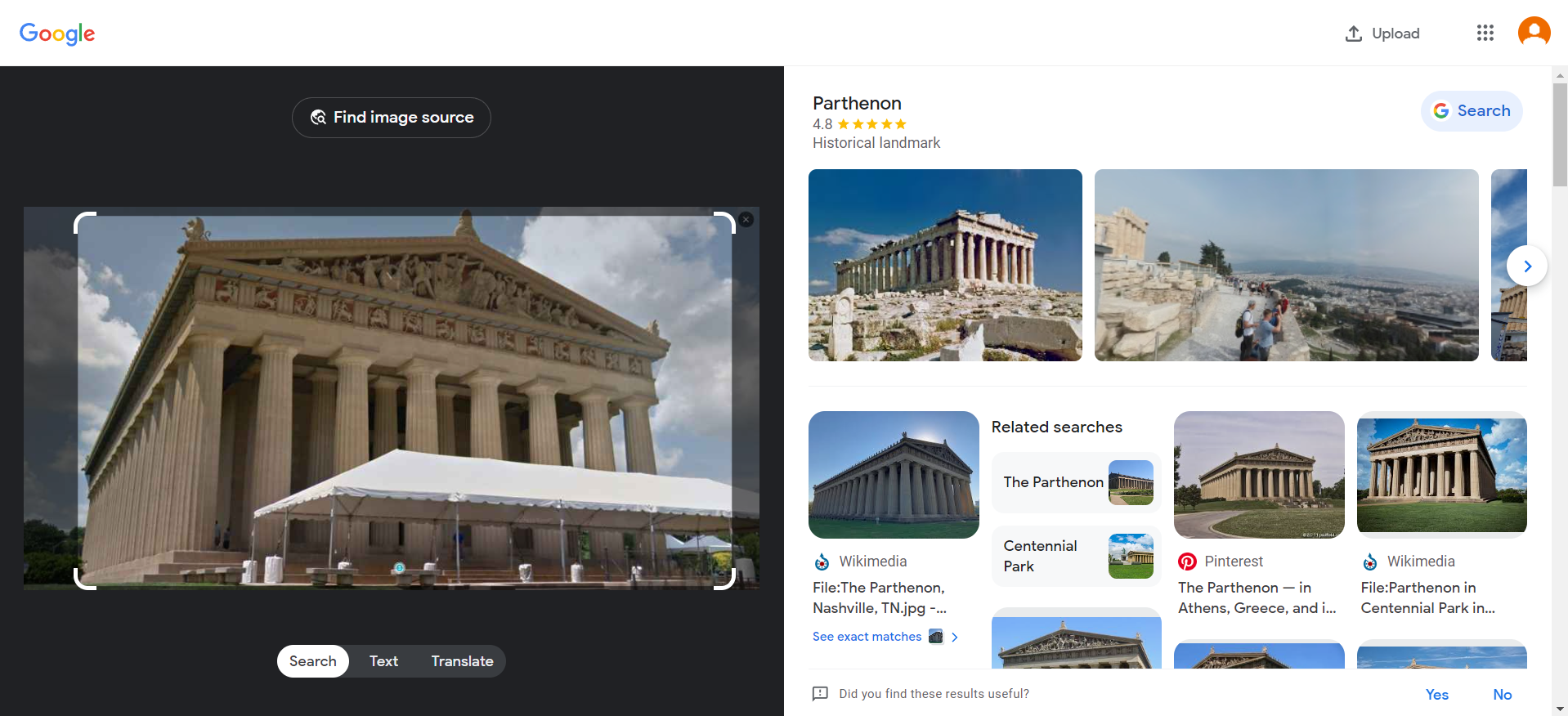
Next, in accordance with the challenge descrition, we utilized What3words. This unique geocoding method is capable of pinpointing places on the surface of the planet with a resolution of around 3 meters.

FLAG
squ1rrel{half.blues.number}
Rev
Secret Coffee Nut Stash
Overview
Description: You’ll never be able to break into my secret Java coffee nut stash!
We are given a .class file and it contains Java bytecode that can be executed, so we just try to run it and the prompt asks to enter a password
$ java CoffeNutStash
Welcome to the Coffee Nut Stash!
Enter the password?
idk
Incorrect password!Afterwards, we can use jd-cli to decompile the .class bytecode into the original source code.
$ dec CoffeNutStash.class
12:05:57.042 INFO com.github.kwart.jd.cli.Main - Decompiling CoffeNutStash.class
import java.util.Scanner;
public class CoffeNutStash {
private static final int[] expected = new int[] {
578, 568, 588, 248, 573, 573, 508, 543, 618, 258,
553, 533, 243, 608, 478, 608, 243, 588, 573, 478,
533, 263, 593, 263, 478, 498, 243, 513, 513, 258,
258, 478, 273, 258, 288, 253, 278, 263, 628 };
public static void main(String[] paramArrayOfString) {
System.out.println("Welcome to the Coffee Nut Stash!");
System.out.println("Enter the password? ");
Scanner scanner = new Scanner(System.in);
String str = scanner.next();
scanner.close();
char[] arrayOfChar = str.toCharArray();
if (arrayOfChar.length != expected.length) {
System.out.println("Incorrect password!");
return;
}
for (byte b = 0; b < arrayOfChar.length; b++) {
char c = arrayOfChar[b];
if (c * 5 + 3 != expected[b]) {
System.out.println("Incorrect password!");
return;
}
}
System.out.println("Correct!");
}
}From the source code, that each character of the password, when multiplied by 5 and added to 3, should equal the corresponding value in the expected array. We can reverse this operation for each value in the expected array.
1expected = [578, 568, 588, 248, 573, 573, 508, 543, 618, 258, 553, 533, 243, 608, 478, 608, 243, 588, 573, 478, 533, 263, 593, 263, 478, 498, 243, 513, 513, 258, 258, 478, 273, 258, 288, 253, 278, 263, 628]
2password = ''.join(chr((n - 3) // 5) for n in expected)
3print(password)And run it
$ python3 solver.py
squ1rrel{3nj0y_y0ur_j4v4_c0ff33_639274}FLAG
squ1rrel{3nj0y_y0ur_j4v4_c0ff33_639274}
PYC Fun
Next rev challenge is python bytecode, I use pycdc to decompile it right away.
$ pycdc pyc_fun.pyc
# Source Generated with Decompyle++
# File: pyc_fun.pyc (Python 3.11)
Unsupported opcode: JUMP_BACKWARD
key = [
44,
56,
247,
253,
233,
88,
109,
105,
57,
67,
28,
46,
17,
166,
155,
71,
129,
255,
155,
81,
144,
109,
110,
2,
151,
97,
172,
93,
185,
41,
67,
212]
result = [
3807,
2927,
7947,
5457,
6217,
1682,
317,
197,
2647,
2042,
4052,
3087,
3127,
8507,
6742,
1962,
8907,
8267,
9312,
557,
9872,
957,
-3,
3727,
6502,
3487,
7947,
2402,
5657,
3167,
2202,
6782]
flag = input()
# WARNING: Decompyle incompleteNah.. It seems the decompilation process is incomplete due to an unsupported opcode: JUMP_BACKWARD.
Reluctantly, we used pycdas to disassemble it, and performed static analysis to get the original source code,
$ pycdas pyc_fun.pyc
pyc_fun.pyc (Python 3.11)
[Code]
File Name: chal.py
Object Name: <module>
Qualified Name: <module>
Arg Count: 0
Pos Only Arg Count: 0
KW Only Arg Count: 0
Stack Size: 5
Flags: 0x00000000
[Names]
'key'
'result'
'input'
'flag'
'zip'
'r'
'k'
'c'
'ord'
'val'
'print'
'exit'
[Locals+Names]
[Constants]
(
44
56
247
253
233
88
109
105
57
67
28
46
17
166
155
71
129
255
155
81
144
109
110
2
151
97
172
93
185
41
67
212
)
(
3807
2927
7947
5457
6217
1682
317
197
2647
2042
4052
3087
3127
8507
6742
1962
8907
8267
9312
557
9872
957
-3
3727
6502
3487
7947
2402
5657
3167
2202
6782
)
3
5
'Incorrect!'
1
'Correct!'
None
[Disassembly]
0 RESUME 0
2 BUILD_LIST 0
4 LOAD_CONST 0: (44, 56, 247, 253, 233, 88, 109, 105, 57, 67, 28, 46, 17, 166, 155, 71, 129, 255, 155, 81, 144, 109, 110, 2, 151, 97, 172, 93, 185, 41, 67, 212)
6 LIST_EXTEND 1
8 STORE_NAME 0: key
10 BUILD_LIST 0
12 LOAD_CONST 1: (3807, 2927, 7947, 5457, 6217, 1682, 317, 197, 2647, 2042, 4052, 3087, 3127, 8507, 6742, 1962, 8907, 8267, 9312, 557, 9872, 957, -3, 3727, 6502, 3487, 7947, 2402, 5657, 3167, 2202, 6782)
14 LIST_EXTEND 1
16 STORE_NAME 1: result
18 PUSH_NULL
20 LOAD_NAME 2: input
22 PRECALL 0
26 CALL 0
36 STORE_NAME 3: flag
38 PUSH_NULL
40 LOAD_NAME 4: zip
42 LOAD_NAME 1: result
44 LOAD_NAME 0: key
46 LOAD_NAME 3: flag
48 PRECALL 3
52 CALL 3
62 GET_ITER
64 FOR_ITER 67 (to 200)
66 UNPACK_SEQUENCE 3
70 STORE_NAME 5: r
72 STORE_NAME 6: k
74 STORE_NAME 7: c
76 PUSH_NULL
78 LOAD_NAME 8: ord
80 LOAD_NAME 7: c
82 PRECALL 1
86 CALL 1
96 LOAD_NAME 6: k
98 BINARY_OP 12 (^)
102 STORE_NAME 9: val
104 LOAD_NAME 9: val
106 LOAD_CONST 2: 3
108 BINARY_OP 3 (<<)
112 LOAD_NAME 9: val
114 LOAD_CONST 3: 5
116 BINARY_OP 9 (>>)
120 BINARY_OP 7 (|)
124 STORE_NAME 9: val
126 LOAD_NAME 9: val
128 LOAD_CONST 3: 5
130 BINARY_OP 5 (*)
134 LOAD_CONST 2: 3
136 BINARY_OP 10 (-)
140 STORE_NAME 9: val
142 LOAD_NAME 9: val
144 LOAD_NAME 5: r
146 COMPARE_OP 3 (!=)
152 POP_JUMP_FORWARD_IF_FALSE 22 (to 198)
154 PUSH_NULL
156 LOAD_NAME 10: print
158 LOAD_CONST 4: 'Incorrect!'
160 PRECALL 1
164 CALL 1
174 POP_TOP
176 PUSH_NULL
178 LOAD_NAME 11: exit
180 LOAD_CONST 5: 1
182 PRECALL 1
186 CALL 1
196 POP_TOP
198 JUMP_BACKWARD 68
200 PUSH_NULL
202 LOAD_NAME 10: print
204 LOAD_CONST 6: 'Correct!'
206 PRECALL 1
210 CALL 1
220 POP_TOP
222 LOAD_CONST 7: None
224 RETURN_VALUEAnd here’s the last result,
1key = [44, 56, 247, 253, 233, 88, 109, 105, 57, 67, 28, 46, 17, 166, 155, 71, 129, 255, 155, 81, 144, 109, 110, 2, 151, 97, 172, 93, 185, 41, 67, 212]
2result = [3807, 2927, 7947, 5457, 6217, 1682, 317, 197, 2647, 2042, 4052, 3087, 3127, 8507, 6742, 1962, 8907, 8267, 9312, 557, 9872, 957, -3, 3727, 6502, 3487, 7947, 2402, 5657, 3167, 2202, 6782]
3
4flag = ''
5
6for r, k in zip(result, key):
7 val = ((r + 3) // 5)
8 val = ((val >> 3) | (val << 5)) & 0xFF
9 c = chr(val ^ k)
10 flag += c
11
12print(flag)$ python3 solve.py
sq1urrel{pyc_r3v_1s_fun_56ja4ft}FLAG
sq1urrel{pyc_r3v_1s_fun_56ja4ft}
